[자바기초.025] Simplifying Boolean Using De Morgan's Law

[자바기초.025] Simplifying Boolean Using De Morgan's Law

 

1.  논리 부정 연산자(negation) !

• 논리 부정 연산자(negation)는 " ! " 로 사용하며, !(true) = false,  !(false) = true와 같이 참과 거짓을 반대로 만든다.
• 그리고 이런 문장이 있다고 가정하자. "나는 고등학교에 있는 선생님이다."
• 이 문장에 !(negation) 논리 뷰정 연산자를 사용한다면, "나는 고등학교에 있는 선생님이 아니다" 라고 표현할 수 있다.
• 그런데, "나는 고등학교에 있는 선생님이 아니다"라는 말은 좀 모호한게, "나는 고등학교가 아니고 다른 중학교나 초등학교를 말하는 건지?", 또는 "나는 고등학교에 있는건 맞는데, 선생님이 아니라는 건지?" 두 가지 내용중에 어느것이 아니(negation)라는 것인지 모호하다.
• 그래서 프로그래밍에서는 !(negation) 논리 연산자를 더 명확하게 나타낼 필요가 있다.

 

2. De Morgan's Law(드 모르간의 법칙)

• De Morgan's Law(드 모르간의 법칙)은 1800년대에 Augustus De Morgan에 의해 개발된 법칙으로서, 복잡한 Boolean expression에 !(negation)을 적용할 때 어떻게 간단하게 나타낼 수 있는지 알려주는 법칙이다.
• and (&&) or or (||), such as (x < 3) && (y > 2)와 같은 Boolean expression에서 !(negation)을 적용할 때는 단순히 and, or 을 서로 뒤집거나 < , > 의 범위를 반대 범위로 바꿔주면 된다.
• 드 모르간 법칙의 자세한 예시는 아래와 같다.

드 모르간 법칙

 

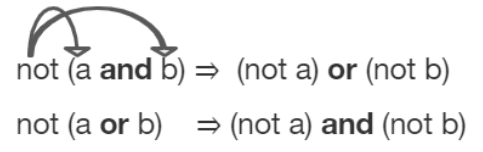
3.자바에서 드 모르간 법칙의 예시

• !(a && b) is equivalent to !a || !b
• !(a || b) is equivalent to !a && !b
• !(c == d) is equivalent to c != d
• !(c != d) is equivalent to c == d
• !(c < d) is equivalent to c >= d
• !(c > d) is equivalent to c <= d
• !(c <= d) is equivalent to c > d
• !(c >= d) is equivalent to c < d

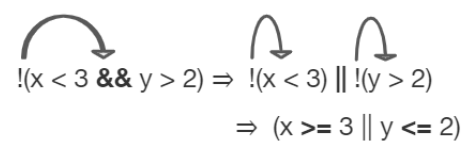
!(a && b) is equivalent to !a || !b

a = "teacher"
b = "at our high school"

Going back to our example above, !(a teacher && at our high school) is equivalent to !(a senior) or !(at our high school) using De Morgan’s Laws:

 

 

< Truth Table >

 

4. 코딩 실습으로 De Morgan's Law 연습하기

[문제1] 아래의 Boolean expression (A)를 드 모르간 법칙으로 간단히 만들어 다시 한번 실행해 보세요.

그리고 결과값이 true가 나오려면 변수  x, y의 값으로 알맞은 것을 아무거나 수정해 보세요.

int x = 2;
int y = 3;
System.out.println(!(x < 3 && y > 2)); // (A)
// simplifying (A) using De Morgan's Law and print again;

 

 

[문제2] 아래 코드의 실행 결과는?

int x = 4, y = 3;
if (!(x < 3 || y > 2))
{
   System.out.println("first case");
}
else
{
   System.out.println("second case");
}

 

A. first case
B. second case

 

 

[문제3] 아래의 Boolean expression과 같은 것을 고르세요.

!(x > 2 && y < 4)

 

A. (x < 2) || (y > 4)

B. (x < 2) && (y > 4)

C. (x <= 2) || (y >= 4)

D. (x <= 2) && (y >= 4)

 

 

[문제4] 아래 Boolean expression과 같은 것을 고르세요.

!(x == 2 && y > 4)

 

A. (x != 2) || (y < 4)

B. (x != 2) && (y < 4)

C. (x != 2) && (y <= 4)

D. (x != 2) || (y <= 4)

 

 

[문제5] 아래 Boolean expression과 같은 것을 고르세요.

!(x!=5 && y!=7)

 

A. (x == 5) || (y == 7)

B. (x == 5) && (y == 7)

C. (x != 5) || (y != 7)

D. (x < 5) || (x > 5) || (y > 7) || (y < 7)

 

 

[문제6] 아래 Boolean expression과 같은 것을 고르세요.

!(x<= 5 && y > 7)

 

A. (x > 5) && (y < 7)

B. (x > 5) || (y < 7)

C. (x > 5) && (y <= 7)

D. (x > 5) || (y <= 7)

 

---

 

[문제 정답은 아래 "더보기" 클릭]

[문제1 정답]

int x = 4;
int y = 3;
System.out.println(!(x < 3 && y > 2)); // (A)
// simplifying (A) using De Morgan's Law and print again;
System.out.println(x >= 3 || y <= 2);

 

[문제2 정답]

 B. second case

 

[문제3 정답]

 C

 

[문제4 정답]

D

 

[문제5 정답]

A

 

[문제6 정답]

D